reading-notes

Big O Notation & Pain

Big O Notaion

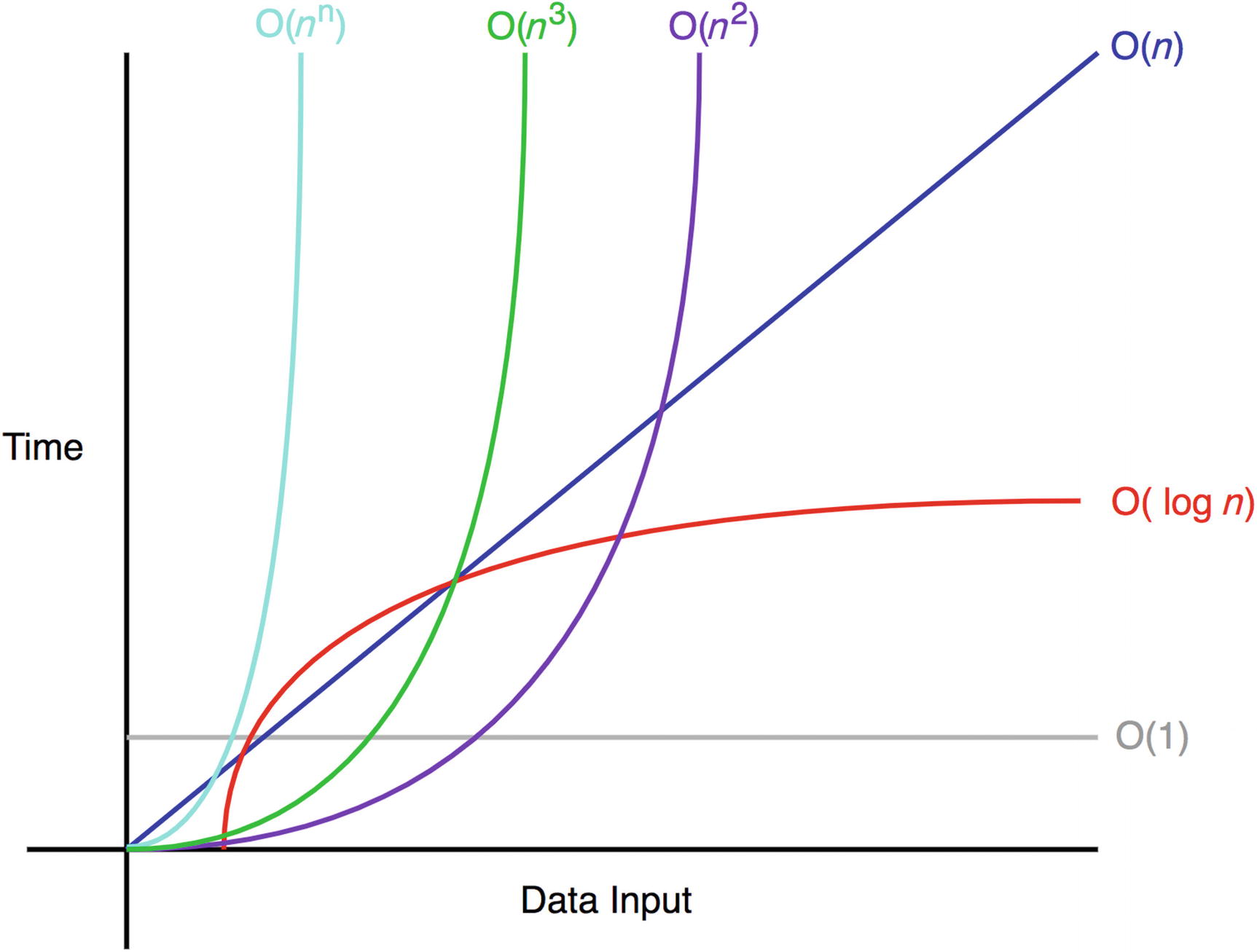
Big O notation describes the performance or complexity of an algorithm. so it indicates the time and memory a code will take to execute, the best case is reaching log(n) since it takes the least time and space

the orders of the big O Notation are:

O(1)

it describes the case when code will executes in the same time and space no matter what’s the inputs (constant), example:

def fact2(n):

if n == 0:
    return 1
else:
    return n * fact2(n-1)

print (fact2(5))

O(N)

O(N) describes an algorithm whose performance will grow linearly and in direct proportion to the size of the input data set. for example:

def fact(n):

product = 1
for i in range(n):
    product = product * (i+1)
return product

print (fact(5))

O(N²)

O(N²) represents an algorithm whose performance is directly proportional to the square of the size of the input data set. example:

a = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]

for i in a:

for x in a:
    print("x")

O(2^N)

O(2^N) denotes an algorithm whose growth doubles with each addition to the input data set. Example

int Fibonacci(int number)

{

if (number <= 1) return number;
   
return Fibonacci(number - 2) + Fibonacci(number - 1);  `}`

Logarithms

This type of algorithm is described as O(log N). The iterative halving of data sets described in the binary search example produces a growth curve that peaks at the beginning and slowly flattens out as the size of the data sets increase

the graph below summarizes the oreders of the big O notation:

## Pain vs. Suffering

• the article talks about the efforts that 401 students have to do in order to obtain the best results
• it talks about how it’s going to be a painful journey but we have to exceed our limits so we could be competent programmers
• it also talks about how we should deal and live with this pain

always remember through this pain these questions:

• What’s your perspective?
• Why are you doing this? -Do you want what comes at the end of this journey?
• Are you doing this for you?